前言

这阵子读论文遇到了MinHash,LSH 两个新的概念，一开始还有点不好消化，网上的文章写的也是五花八门，因此，根据自己的理解撰写一篇笔记，方便日后回看。

MinHash

要了解一个概念首先要从提出概念的问题开始，在自然语言或其他特征工程当中，我们经常会遇到多维度的特征向量（用于表征一个集合或文档），有的可能十几个特征，有的可能成百上千，对于两个特征向量，我们常常需要计算它们之间的相似度（如文档的相似性），计算的方法有很多，以Jaccard相似度为例：

$$Jaccard(A,B) = \frac{c}{a+b-c}$$

其中，c是A,B中共同非零的特征个数，a,b分别为A,B中非零的特征个数。

我们重点关注的是计算的效率，如果每一维特征之间都要一一计算，这样的话随着特征维度的增加，计算复杂度会大幅上升，并且，我们真正关心的不是局部某个特征的差异，而是全局两个特征向量。因此，就考虑将原本非常大的特征向量映射到一个低维空间上，使得低维空间中两个向量之间的相似性接近原始特征向量的相似性，这就是MinHash的思想，得到的低维空间向量就是hash值。如下：

$$A=(a_1,a_2,...,a_n)\to A' =(a'_1,...,a'_m)$$ $$B=(b_1,b_2,...,b_n)\to B'=(b'_1,...,b'_m)$$ $$diff(A,B) \approx diff(A',B')$$

之所以是约等于是映射的过程中必然丢弃一些特征信息

那么，哪些是可以被丢弃的呢？显而易见，稀疏向量中的0。

先说一下MinHash的思想：

1. 对文档(A,B,C,D)对应特征的行进行重排列
2. 取排列后每列（对应文档）的第一个非零值即为MinHash
3. 重复多次1-2步骤，得到原特征向量的新表示，称signature，即降维后的新向量
4. 计算两个signature之间相等值的比例，即得到近似Jaccard相似度

对原理解释一下，我们对任意的两个特征向量A,B，它们在任意衣一行上的特征取值有三种情况：

• 均为1：总数记为x
• 一个为1，一个为0，总数记为y
• 均为0：两者均不考虑，跳过

那么两个向量MinHash相等的概率即为$\frac{x}{x+y}$，再看Jaccard的计算，显然有$Jaccard(A,B) = \frac{x}{x+y}$，因此

$$P(MinHash(A)=MinHash(B)) = Jaccard(A,B)$$

但由于前者是概率，在实际计算中，我们需要计算多次（即多个MinHash），实现对Jaccard的估计。

这部分可以理解为抛硬币的理论正面概率为1/2，实际测试概率需要多次实验计算抛掷结果为正面的比例

当我们计算m次MinHash后，A，B分别得到由MinHash组成的两个新低维向量$sig(A)=(h1(A), h2(A), …, h_m(A)), sig(B)=(h1(B), h2(B), …, h_m(B))$，接着只需要计算两个向量中相等值的比例就得到了估计的Jaccard

其中$h_i$表示第i个MinHash函数

举个例子，有4个特征向量$A(0,1,1,0),B(0,1,0,1),C(1,0,1,0),D(0,1,1,1)$，用矩阵表示如下：

	A	B	C	D
1	0	0	1	0
2	1	1	0	1
3	1	0	1	1
4	0	1	0	1

例如将第4行换到第1行（重排列）: 注意下划线1对应每列第一个非零行

	A	B	C	D
1	0	1	0	1
2	0	0	1	0
3	1	1	0	1
4	1	0	1	1

此时得到(A,B,C,D)对应MinHash为(3,1,2,1)

如果仅用此代表原来的文档，则得出结论，B，D最相似，其他两两不相似，事实上A,D也有一般特征相同，这是因为特征丢弃太多导致

用同样的方法，这次我们交换1-2行（在原特征向量的基础上）

	A	B	C	D
1	1	1	0	1
2	0	0	1	0
3	1	0	1	1
4	0	1	0	1

此时得到对应MinHash为(1,1,2,1)，与上面的特征结合，得到A,B,C,D的低维表示(signature matrix)：

	A	B	C	D
1	3	1	2	1
2	1	1	2	1

A,D的相似度从0%到了50%。

仔细观察上面的重新排列，本质上是对行进行了映射，第一次是$(1,2,3,4)\to(4,1,2,3)$, 第二次是$(1,2,3,4)\to(2,1,3,4)$，映射的操作可以通过hash函数模拟实现。

之所以将重排列换成hash是因为hash的计算成本比全排列要低得多

下面是用hash替代重排列计算signature的算法步骤：

for each row r do begin
    for each hash function hi do
        compute hi(r)
    for each column c
        if c has 1 in row r
            for each hash function hi do
                if hi(r) < M(i,c) then
                    M(i,c) := hi(r)
end

解读一下：首先我们需要准备一些hash function，例如h1(x) = x%m+1, h2(x)=2*x%m +2（m是行数），对每一行（行号）计算其被每个hash function hash得到的值（这相当于是做了重排列，因为行号通过hash从原始行映射到了一个新行），按照原本MinHash的思路，我们应该在hash得到的新行中按照新行号(1-m)顺序取最先的非零值，转换到算法中就是第三个for循环做的事情。对每一列（就是每个文档），计算其MinHash, M(i,c)(i指行号)，只关心那些包含非零值的行，然后看这个行的行号和现有的M(i,c)谁小（小说明重排列后的位置靠前），然后用较小值更新M(i,c)

上面的方法可以说很巧妙地避开了复杂的重排列计算，值得细细品味。

用hash替代排列的例子，可以参考^[1]，或者如下我从网上^[2]摘录的例子，这里不再重复。

对于MinHash，有两点需要说明：

1. hash函数（低维特征数）的增加会提高计算特征向量之间的精确性，但实际问题中很多向量是稀疏的，因此因为降维导致的相似度差异可以忽略
2. 采用hash难免会有碰撞，但当数量级很大时，这部分的影响也可以忽略

LSH

MinHash降低了两个高维向量之间的计算复杂性，但还有一个需要考虑的问题是，我们需要对大量的向量之间进行两两比较，如果每个都直接比较，复杂度是$O(N^2)$（N是向量个数），是否有一种方法，将潜在的可能相似度高的向量聚在一起，将相似度低的向量分开？

LSH(Locality Sensitive Hashing)做的就是这个事情，其基本思想为：我们不需要去比对所有的文档，将所有的文档(columns) hash到许多桶中，形成候选匹配对，只有同一个桶中的signature会进行匹配

---

这里我们需要定义一个相似的标准，即认为两文档相似，应该分到一个桶中的阈值，设为t，只有两个文档的Jaccard值超过t才会被分到一个桶中。

LSH基于此，将原signature matrix按行划分成多个band，每个band的宽度是r，显然有b*r=num of hash function for MinHash，然后对band内每个signature段hash，形成多个桶，如下图:

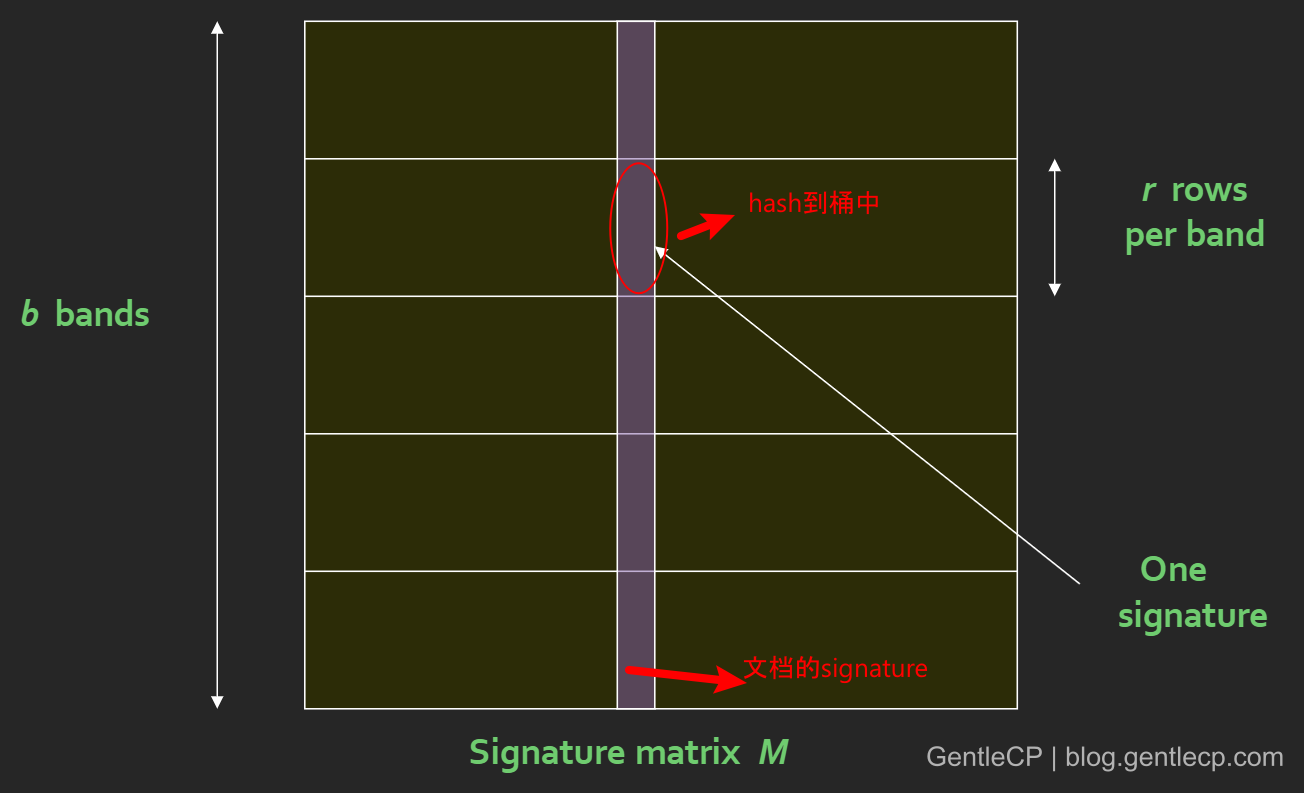
两个文档作为候选匹配的充要条件是至少有一个band的hash在同一个桶中

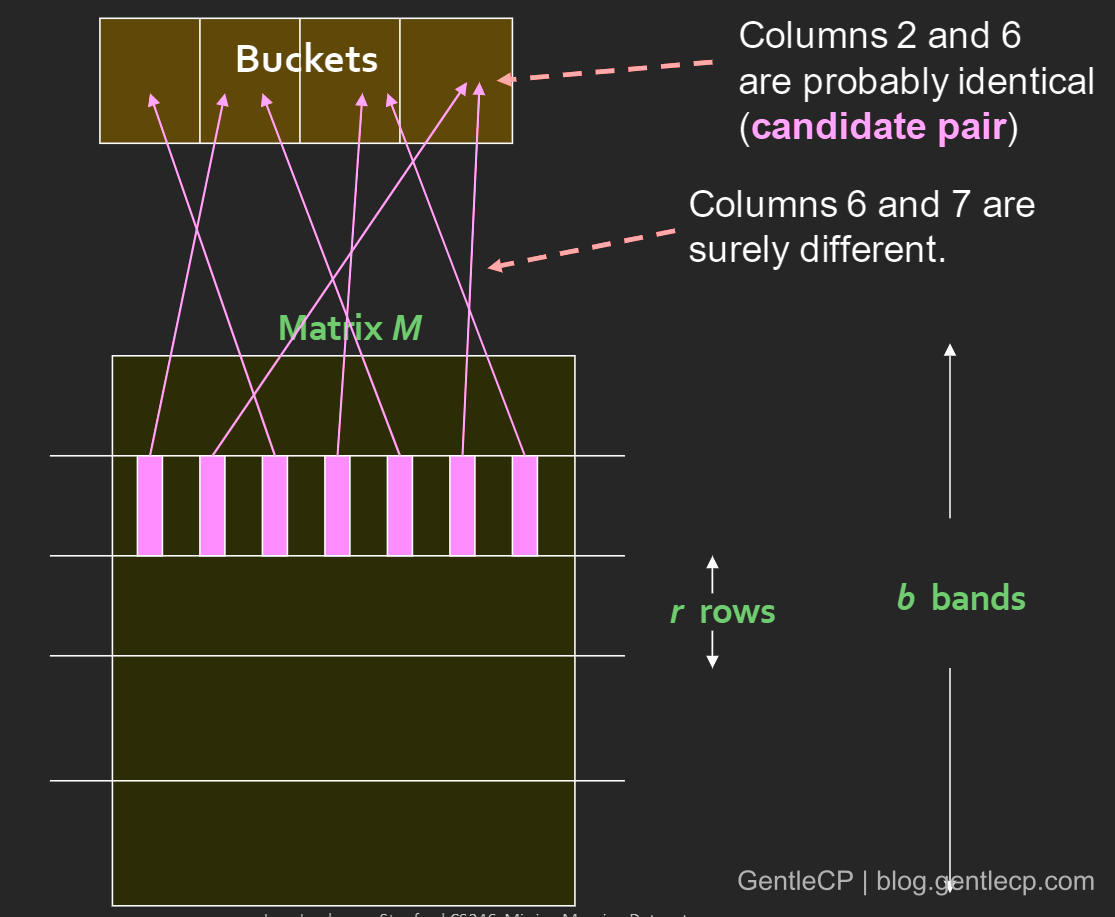
每个band对应的桶是独立的，不影响

为什么上面这种用局部hash去猜测全局相似性的方法可行呢？还记得之前说的两个MinHash相等的概率等于Jaccard（两个文档的相似度），而MinHash相等意味着两者会被hash到同一个桶，因此相似度Jaccard越高，hash到同一个桶的概率也越高，同时呈现线性关系，如下图：

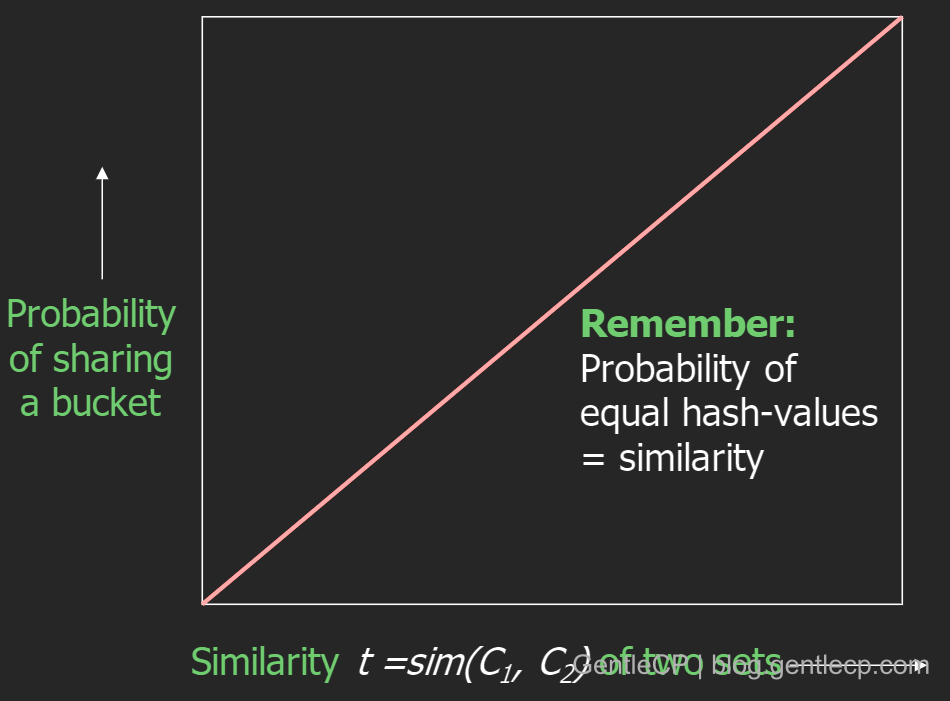
当我们确定了相似度阈值t,但hash分桶的时候仍然存在可能分错桶的情况，分别是：

• 本应认定不相似的分到了一个桶中：因为有小部分MinHash会相当的概率
• 本应认定相似的没分到一个桶中：每个band Hash的结果刚好都不一样

对应如下图区域所示：

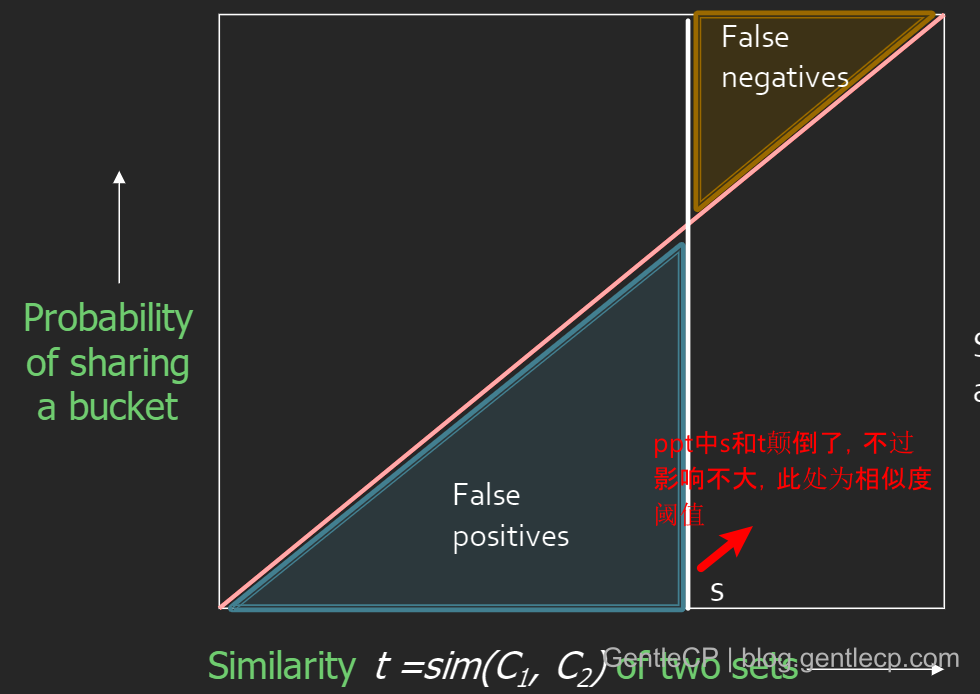
造成这种情况的原因是在对band的划分和hash function的数量(r*b)，具体体现就是参数r,b。因此我们需要对这两者的选取进行调整，设s代表两个文档相似度（对应MinHash相同的概率），那么有：

• 一个band内所有行都相等的概率是$s^r$
• 一个band内至少有一行(一个MinHash)不相等的概率: $1-s^r$
• 所有band都不相等的概率：$(1-s^r)^b$
• 至少有一个band相等的概率；$1-(1-s^r)^b$

最后一个实际上就对应文档被划分到一个桶中的概率，看一组当两文档相似读不同时，其对应概率的变化(取r=5,b=20)：

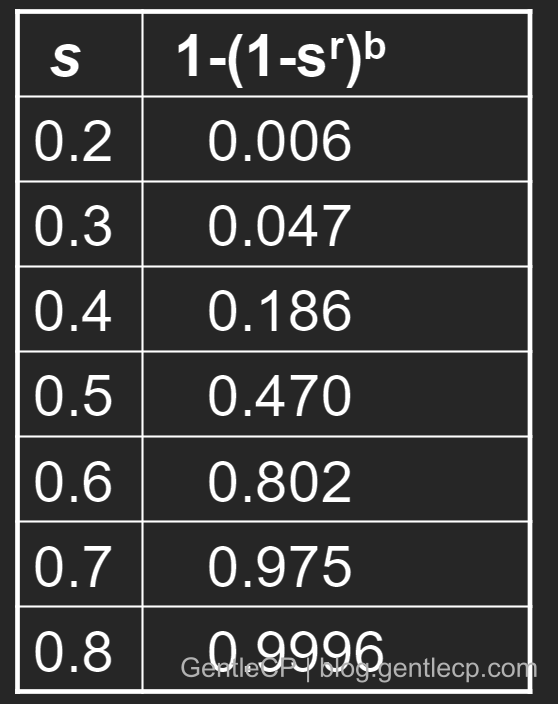
可以看出，相似度越大，越容易被hash到同一个桶中。但前面我们说了有个相似度阈值t，作为两文档是否相似的判定标准，它并不是说t=s=0.5来二分，实际上t是根据该函数$f(s)= 1-(1-s^r)^b$跃阶的点确定的，如下图：

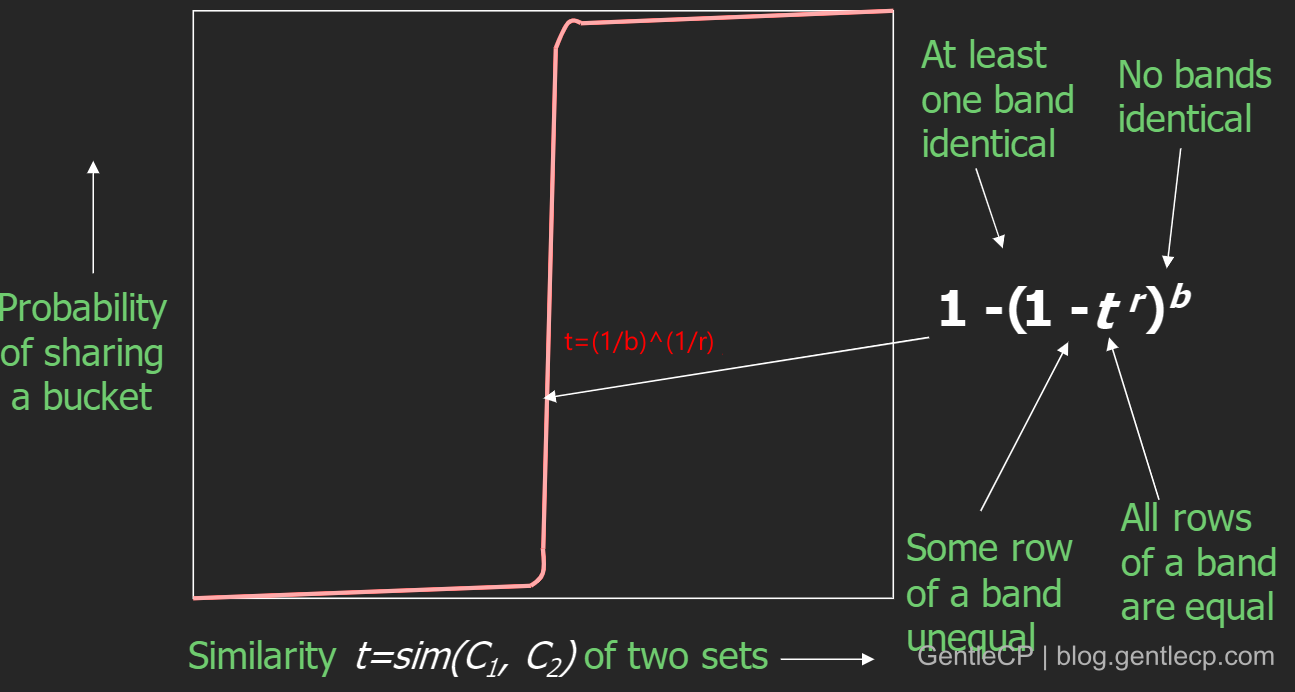
在图中标注的位置是函数跳跃最大的，换句话说就是导数最大的地方，因此应该将阈值设定在这个地方

由上我们可以知道，通过分段hash然后再对在一个桶中的候选signature进行相似度计算，这种方式可以在一定程度上保留对相似度的估计，同时大幅提升计算的效率（因为只需要匹配部分文档）。

还有一个问题就是r,b参数的选取，记得我们的优化方向：

• 避免本应认定不相似的分到了一个桶中：对应就是减小False Positive，提高计算效率，就应该让阈值（即曲线最陡处）较大，这样那些相似性较低的就难以被分到一个桶中，但同时也会筛除一些潜在相似用户，降低了准确率。
• 避免本应认定相似的没分到一个桶中：对应就是减小False Negative，提高准确率，就应该让阈值（即曲线最陡处）较小（如小于我们心中期望的$s_{min}$），这样所有我们认为应该相似的都会被分到一个桶中，但这显然会带来较大的计算量

上述的选择决定于阈值$t=(\frac{1}{b})^\frac{1}{r}$的取值，因此我们可以通过调整不同的b,r来达到相应的目的。

总结

本文是我看了许多讲述LSH的文章后，加入自己的理解撰写的一篇笔记，其中难免纰漏、错误之处，在阅读的过程中，我也发现网上的文章参差不齐，有的存在断章取义，使得对LSH, MinHash的理解存在偏差，最后是看了斯坦福大学的ppt，视频，并结合各家文章，才对这两者有了基本的理解，相应参考资料都放在了后面，感兴趣的可以自己阅读。

参考

1. 2018-11-15-MinHash原理 - 简书 (jianshu.com) ↩
2. (114) Locality Sensitive Hashing Part 1, Jeffrey D Ullman - YouTube ↩
3. LSH算法 - 知乎 (zhihu.com) ↩
4. 大规模数据的相似度计算：LSH算法 - 知乎 (zhihu.com) ↩